Activation Functions¶
ELU¶
Be the first to contribute!
ReLU¶
A recent invention which stands for Rectified Linear Units. The formula is deceptively simple: \(max(0,z)\). Despite its name and appearance, it’s not linear and provides the same benefits as Sigmoid but with better performance.
| Function | Derivative |
\[\begin{split}R(z) = \begin{Bmatrix} z & z > 0 \\
0 & z <= 0 \end{Bmatrix}\end{split}\]
|
\[\begin{split}R'(z) = \begin{Bmatrix} 1 & z>0 \\
0 & z<0 \end{Bmatrix}\end{split}\]
|
|
|
Pros
- Pro 1
Cons
- Con 1
Further reading
- Deep Sparse Rectifier Neural Networks Glorot et al., (2011)
- Yes You Should Understand Backprop, Karpathy (2016)
LeakyReLU¶
LeakyRelu is a variant of ReLU. Instead of being 0 when \(z < 0\), a leaky ReLU allows a small, non-zero, constant gradient \(\alpha\) (Normally, \(\alpha = 0.01\)). However, the consistency of the benefit across tasks is presently unclear. [1]
Pros
- Pro 1
Cons
- Con 1
Further reading
- Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification, Kaiming He et al. (2015)
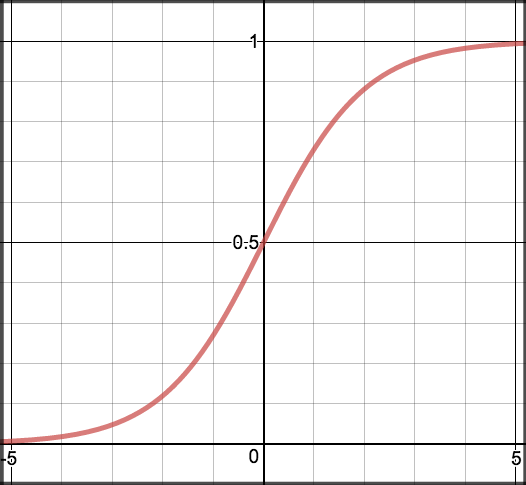
Sigmoid¶
Sigmoid takes a real value as input and outputs another value between 0 and 1. It’s easy to work with and has all the nice properties of activation functions: it’s non-linear, continuously differentiable, monotonic, and has a fixed output range.
| Function | Derivative |
\[S(z) = \frac{1} {1 + e^{-z}}\]
|
\[S'(z) = S(z) \cdot (1 - S(z))\]
|
|
|
Pros
- Pro 1
Cons
- Con 1
Further reading
- Yes You Should Understand Backprop, Karpathy (2016)
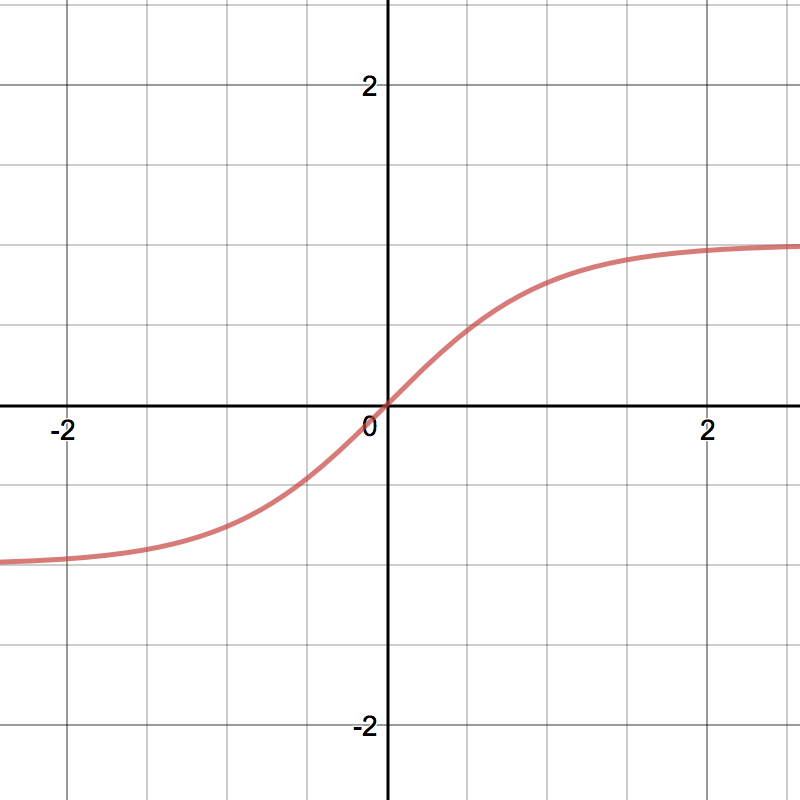
Tanh¶
Tanh squashes a real-valued number to the range [-1, 1]. It’s non-linear. But unlike Sigmoid, its output is zero-centered. Therefore, in practice the tanh non-linearity is always preferred to the sigmoid nonlinearity. [1]
| Function | Derivative |
\[tanh(z) = \frac{e^{z} - e^{-z}}{e^{z} + e^{-z}}\]
|
\[tanh'(z) = 1 - tanh(z)^{2}\]
|
|
|
Pros
- Pro 1
Cons
- Con 1
Softmax¶
Be the first to contribute!
References
| [1] | (1, 2) http://cs231n.github.io/neural-networks-1/ |